Define a Problem

Goals of the project:
* Create 2 trusses that support a heavy load.
* Make the trusses support at least 10 Newtons of force (about 1.02kg)
* Solve both trusses and calculate the individual beam forces.

Generate Concepts

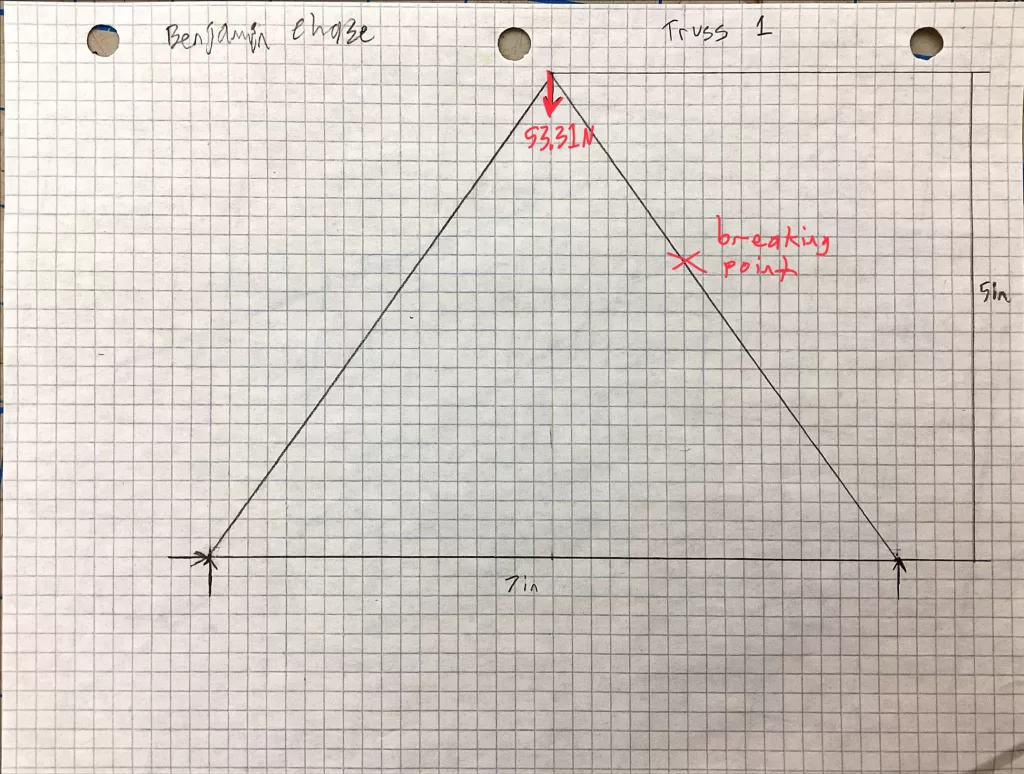
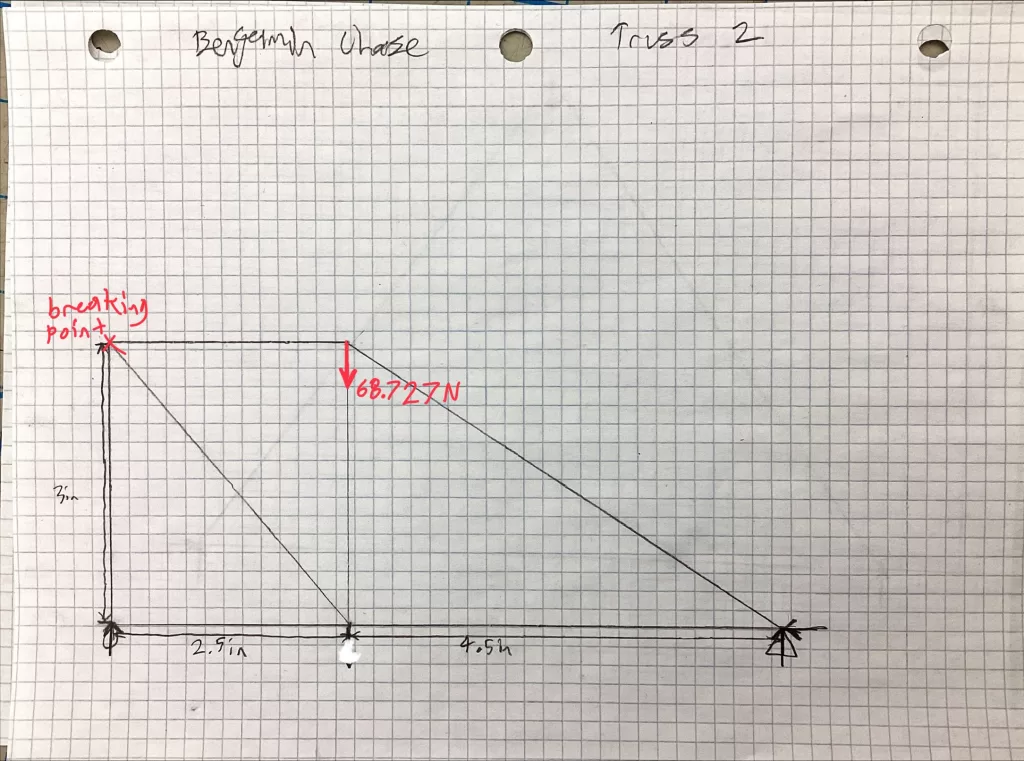
First Truss Expectations:
We expected the first truss to hold a maximum load of 25 Newtons since we used bass wood instead of balsa wood. This means it would hold much more than the average of 3N for balsa wood trusses in the same configuration. Bass wood is much stiffer and stronger than balsa wood, but it is a bit heavier. As a result of this, we expected our efficiency to be slightly greater than that of the other teams. Second Truss Expectations:
Since the second truss had more beams to distribute the weight, we expected it to hold 30 Newtons of force. On the other hand, the basic structure was somewhat similar, and more material and wood glue was used in the design, meaning efficiency would likely decrease.
Static Determinacy:
* The first truss was statically determinate:
2(Joints) = Members + Reactive forces
6 = 3 + 3
6 = 6
True

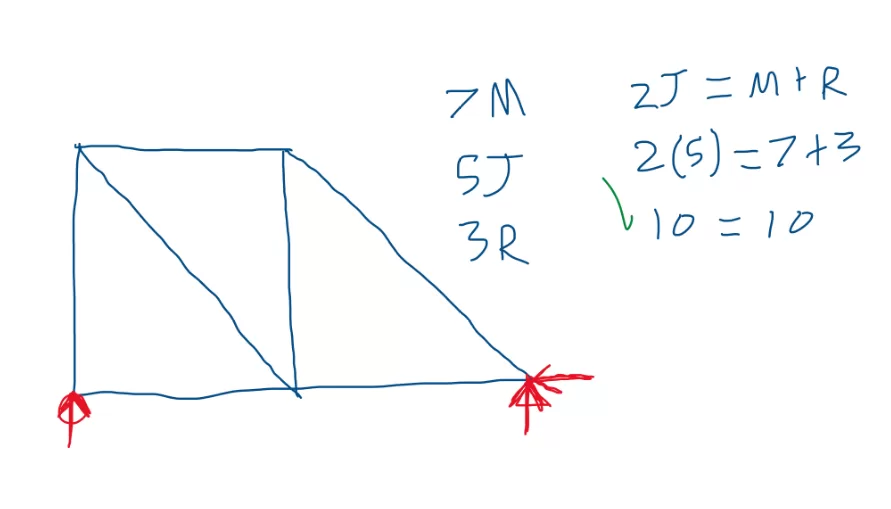
* The second truss was also statically determinate:
2(Joints) = Members + Reactive forces
2(5) = 7 + 3
10 = 10
True

For estimating the maximum loads our trusses could hold, we thought about the stiffness of bass wood and decided that the first truss could hold 25N while the robust second truss could hold 30N of force.

Develop a Solution

First Truss:

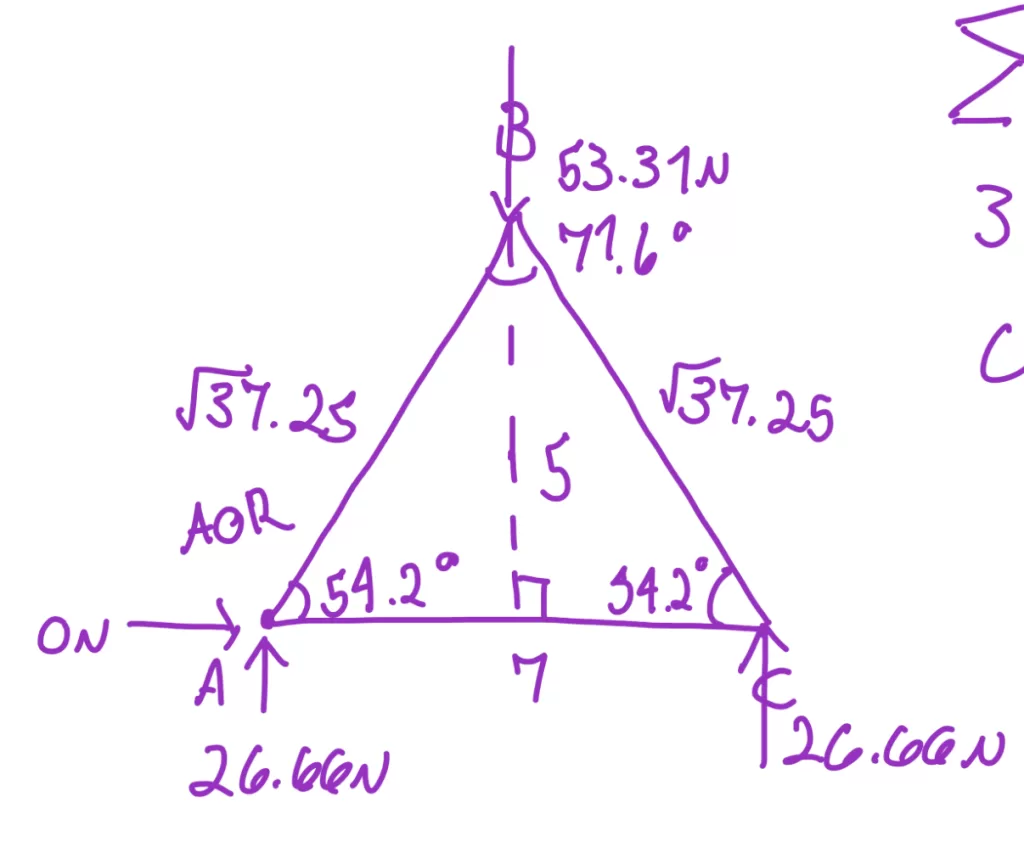
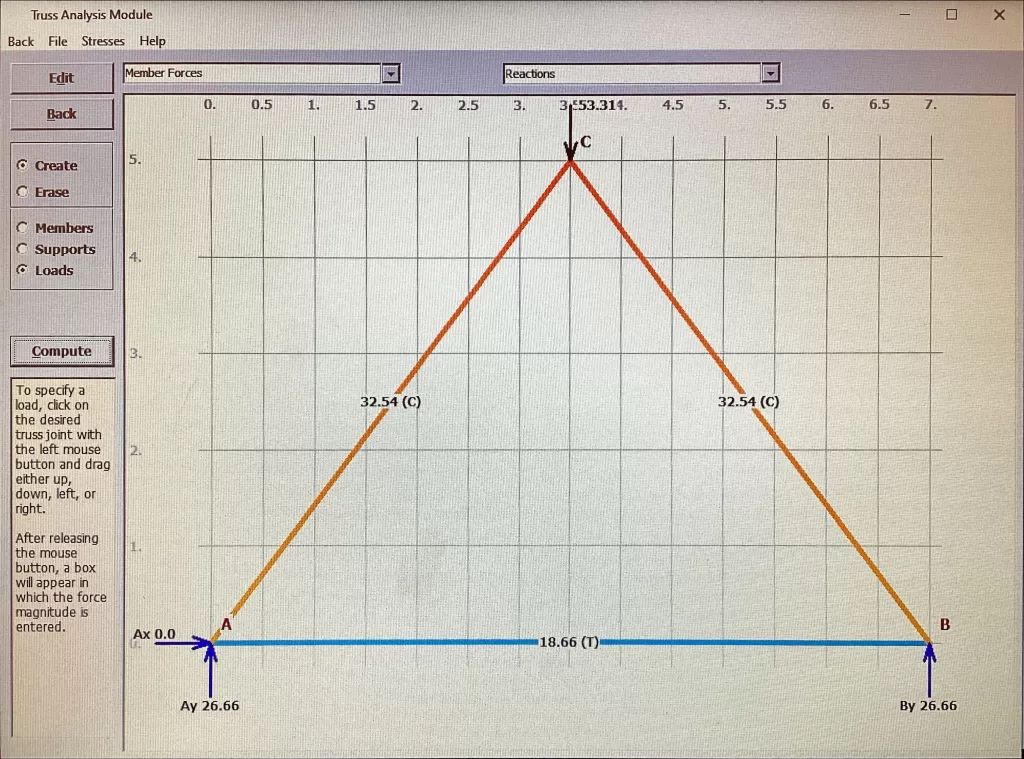
Second Truss:

Construct and Test Prototype

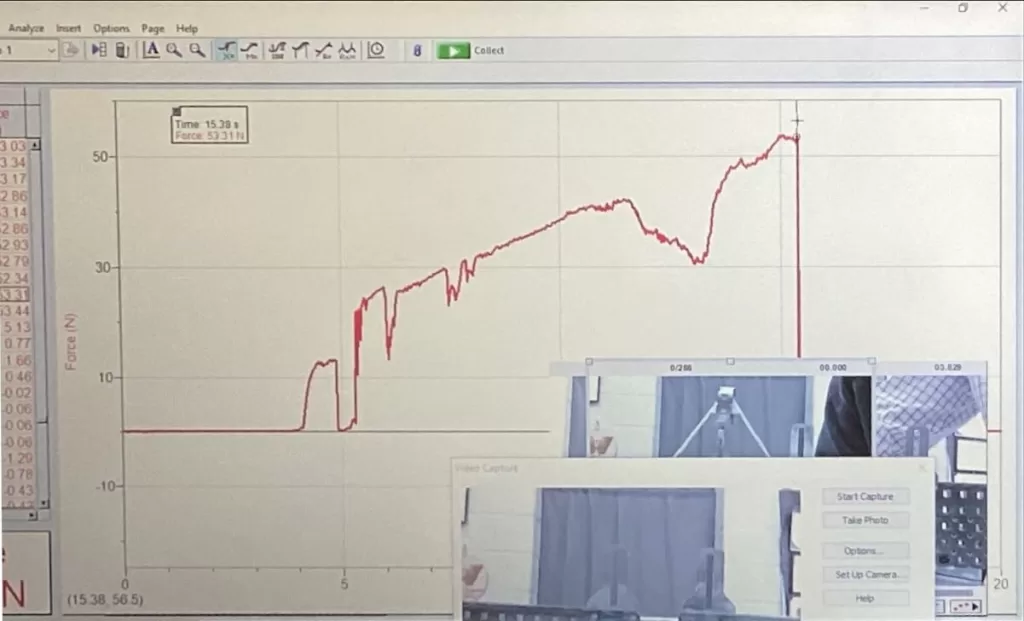
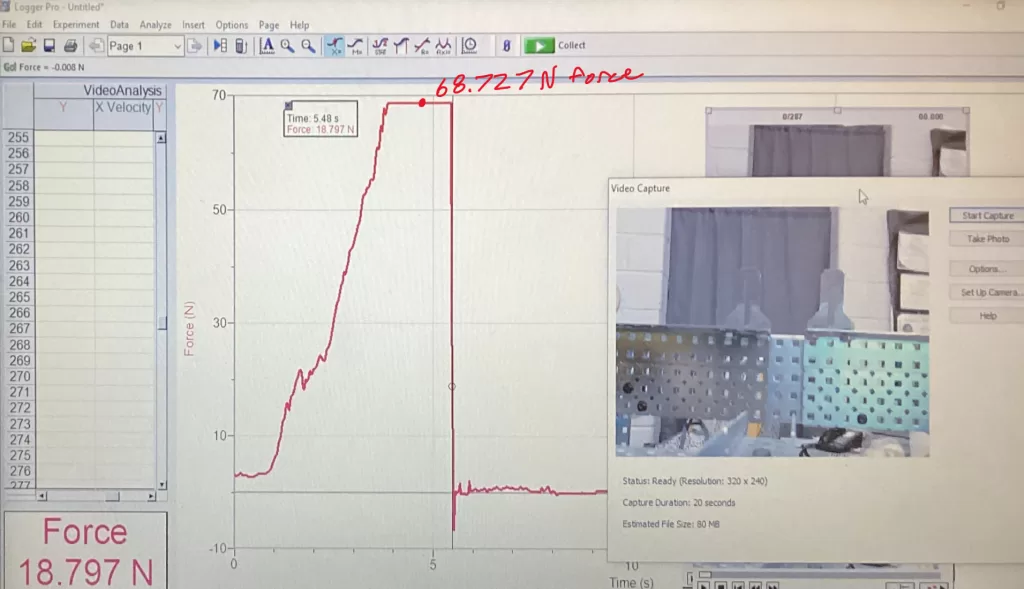
Desktop: Left: Truss 1, Right: Truss 2

Mobile: Top: Truss 1, Bottom: Truss 2

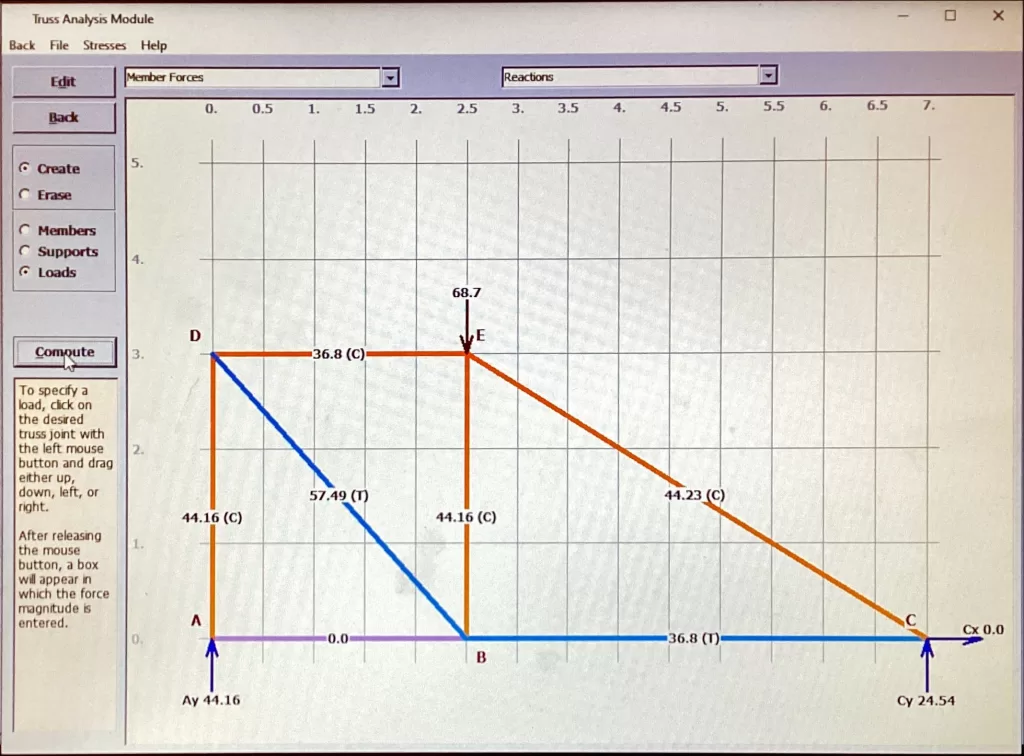
Truss 1 held 53.31N while Truss 2 held 68.7N

Evaluate Solution

Efficiency for Truss 1:
53.31N / 1.6g = 33.32 N/g
Efficiency for Truss 2
68.727N / 2.3g = 29.88 N/g

The first truss is superior to the second truss. This is because it has a much higher efficiency.

33.32 - 29.88 = 3.44

Present Solution

Conclusion

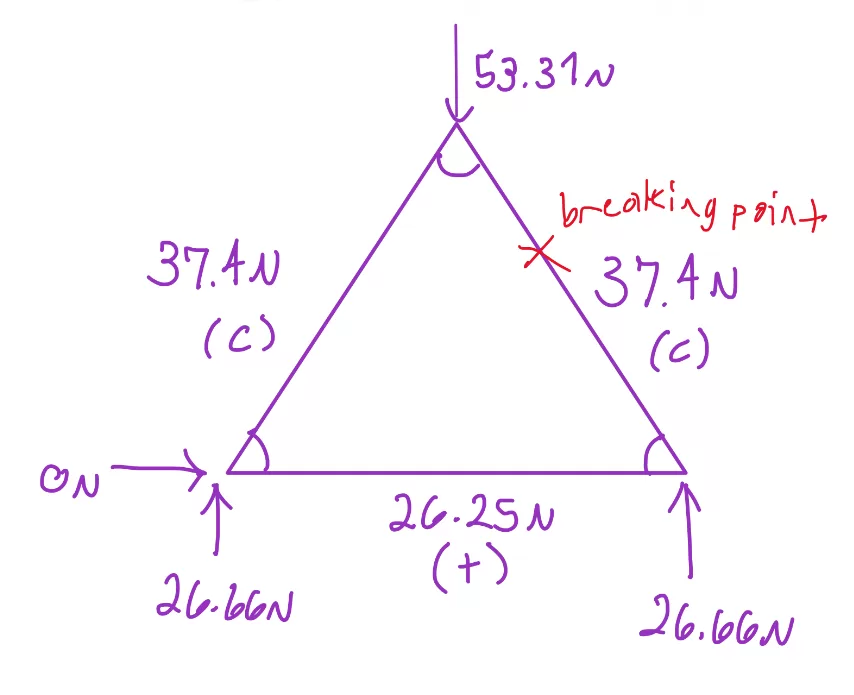
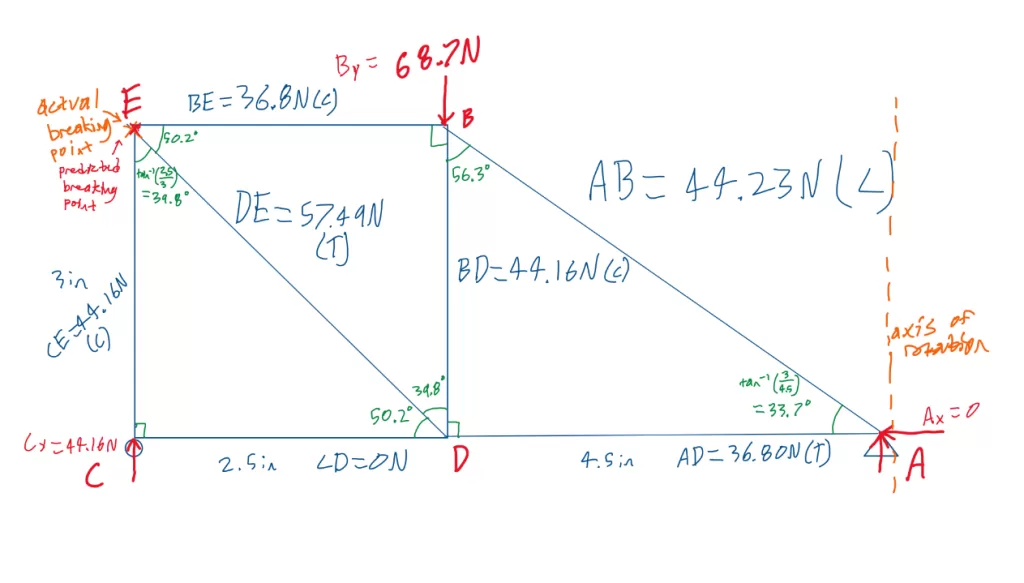
The break point for the first truss was slightly above the center on the right member. This was due to the force of 37.4 N on that member (member BC), which was higher than the force of 26.25 N on member AC. This makes sense since member BC experienced basically the highest amount of force which was only paralleled by member AB, which had the same force applied.

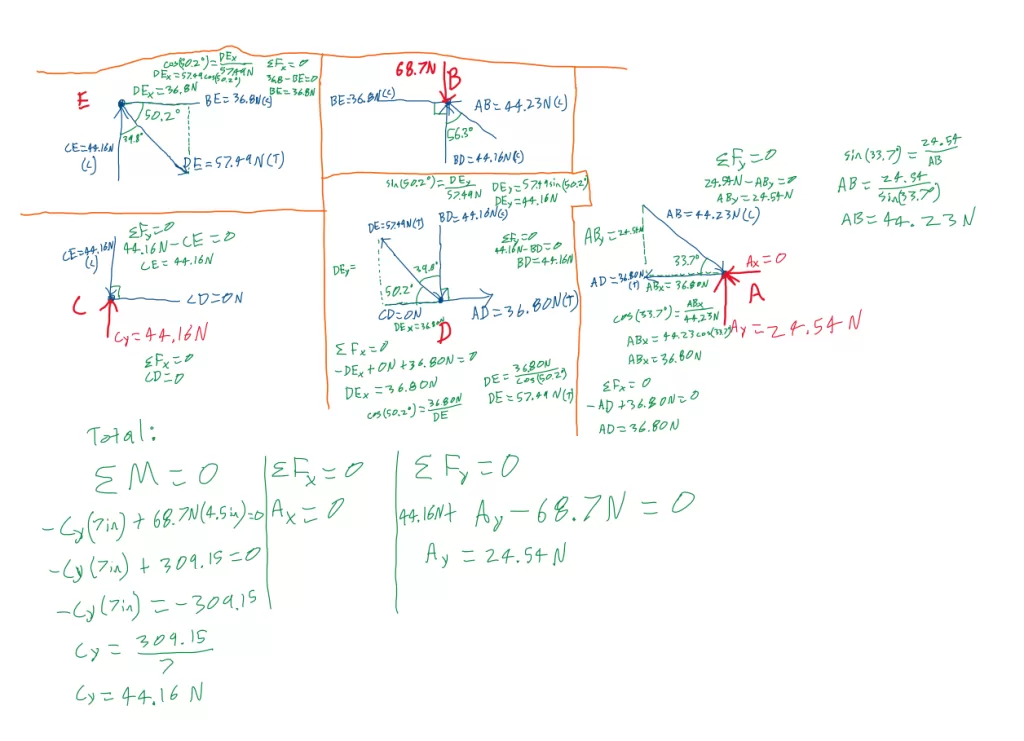
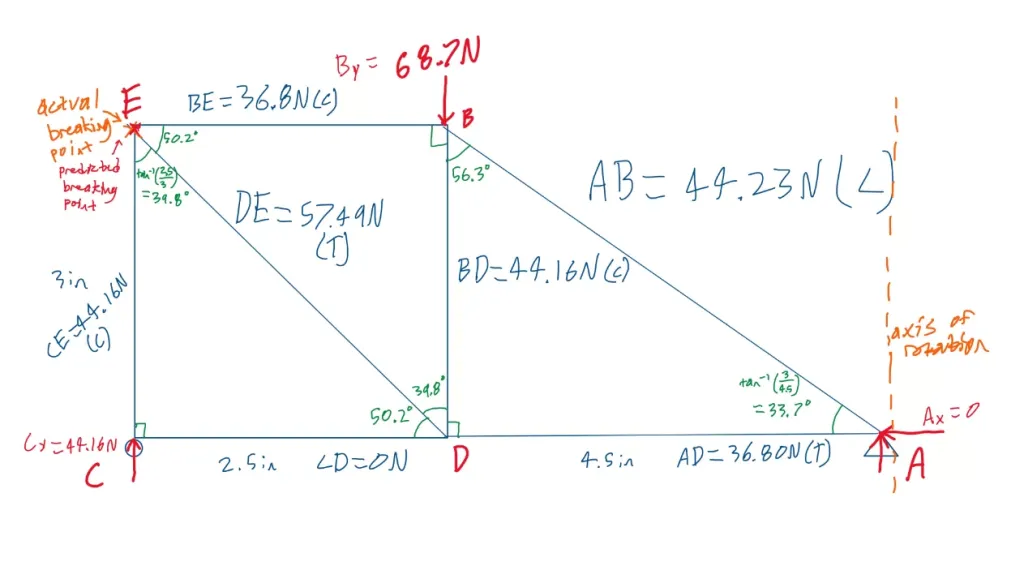
In contrast, the second truss had a quite different design. The second truss failed at joint E, which is logical because 44.16 N in compression were applied at member CE, 57.49 N in tension were applied at member DE, and at BE there were 36.8 N in compression. This joint has forces of the greatest magnitude acting upon it, which means it would be the initial breaking point.
Improvements to the Designs:
* To improve efficiency, I would use paper gusset plates only on joints undergoing tension. This would decrease the weight of the bridge while not affecting the load held. On joints undergoing compression, the paper gussets crumple and do not contribute to the distribution of force across the truss. Taking unnecessary gusset plates off would decrease the weight of the truss, and thus increase its efficiency.

* In addition, I would experiment with different materials, such as balsa wood, different bass wood, oak, or even metals and plastics to find the most efficient material that would best suit this application.

* Wood glue is heavy, so it decreases efficiency. I would like to test super glue and other joining methods to increase efficiency. Even creating wood joints (lap joints, dovetail joints, etc.) could increase the surface area that the glue is applied to, which would increase the strength of the joint, and thus increase efficiency.